4-1

$\sigma(\mathbf w ^\mathsf T \mathbf x +b)$ $\mathbf w$ $\mathbf x$ 恒大于0，其收敛速度会比零均值化的输入更慢

假设这次采用sigmoid作为激活函数

\begin{align} \frac{\partial{L}}{\partial{w}}&=\frac{\partial{L}}{\partial{a}}\cdot\frac{\partial{a}}{\partial{y}}\cdot\frac{\partial{y}}{\partial{w}}\\ &=\frac{\partial{L}}{\partial{a}}\cdot\sigma{(wx)}\cdot(1-\sigma{(wx)})\cdot x \end{align}

$x$ $\frac{\partial{L}}{\partial{a}}$ 有关，所以，各个权重都会向同一个方向更新，造成z型更新的情况

$w_1$ $w_2$ $w_1$ $w_2$ 的梯度符号一致，要么都为正要么都为负，都为正时则往第一象限变化，都为负时则往第三象限变化，而如果此时最优解在第四象限，则实际训练路径会远远长于最短路径，就会使得网络收敛速度变慢。

$w$ $x$ 相关，也就不会全部都一样，也就不会Z型更新了。

4-2

试设计一个前馈神经网络来解决XOR问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用ReLU作为激活函数

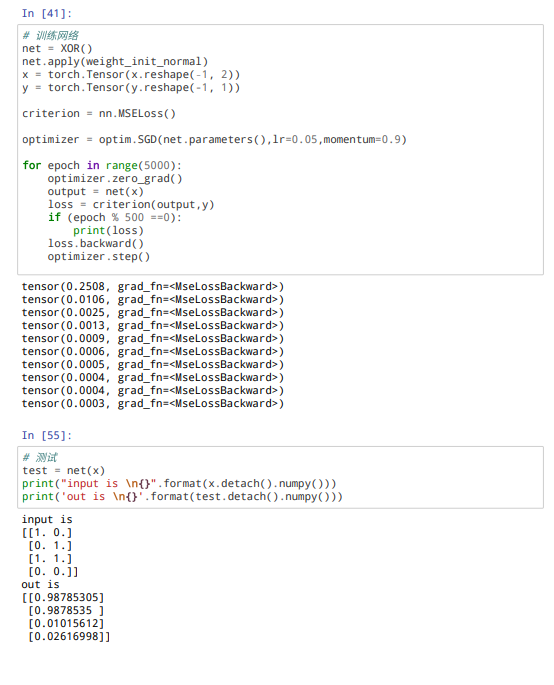
4-3

试举例说明“死亡ReLU问题”，并提出解决方法

举例：

$W$ $2\times 4$ $4\times 1$ 的向量，第二层的激活函数为ReLU

z_1 = \begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} \end{bmatrix}\cdot \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}

如果由于上一次参数更新时，梯度过大，或者学习率设置太大，导致权重一下子更新过多。

就会导致

$z_1 < 0$

$a_1 = ReLU(z_1)=max(z_1)=0$

即激活函数的输出为0

在此次的梯度更新时：

$\frac{\partial{L}}{\partial{z_1}}=\frac{\partial{L}}{\partial{a_1}}\cdot\frac{\partial{a_1}}{\partial{z_1}}=\frac{\partial{L}}{\partial{a_1}}\cdot 0=0$

而

$\frac{\partial{L}}{\partial{W_1}} = \frac{\partial{L}}{\partial{z_1}}\cdot x^\mathsf T = \vec{0}$

也就是说，这几个参数将不再被更新了

解决方法：

把 ReLU换成LeakyReLU ，保证让激活函数在输入小于零的情况下也有非零的输出。
采用较小的学习率
采用 momentum based 优化算法，动态调整学习率

4-5

$M_0$ $L$ $\frac{N}{L}$ $L$ 的关系。

$\frac{N}{L}\cdot M_0 + (L-1)\cdot (\frac{N}{L})^2+N+\frac{N}{L}+1$

4-7

$\mathbf b$ 进行正则化

其实也可以正则化偏置值，但是对于某一隐含层上的神经元来说，权重w是一个高维的参数矩阵，已经可以表达高方差问题，而偏置b仅仅是单个数字，对模型的复杂度影响不大，因此一般选择忽略不计

4-8

$W=0,b=0$ ?

因为如果参数都设为0，在第一遍前向计算的过程中所有的隐藏层神经元的激活值都相同。在反向传播时，所有权重更新也都相同，这样会导致隐藏层神经元没有区分性。这种现象称为对称权重现象。

引用自zhihu

4.9

梯度消失能否通过增加学习率来缓解

在一定程度上能够缓解，但易造成无法收敛等问题