2-1
分析为什么平方损失函数不适用于分类问题
第一,使用平方损失函数意味着我们默认数据服从正态分布,用统计术语来说就意味着我们假设了高斯先验。但很显然,分类问题的数据并不服从正态分布,比如二分类问题则服从伯努利分布。
第二,MSE函数对于分类问题是非凸的。如果使用MSE进行模型训练,则不能保证将Loss函数最小化。
补充
Why Using Mean Squared Error(MSE) Cost Function for Binary Classification is a Bad Idea?
2-2
在线性回归中,如果我们给每个样本赋予一个权重,经验风险函数为
计算其最优参数,并分析权重的作用
对经验风险函数求导,得到 ,另其等于0,即
得到:
2-3
证明在线性回归中,如果样本数量小于特征数量,则的秩最大为
由矩阵秩的定理,可得
得的秩最大为N
2-4
在线性回归中,验证岭回归的解为结构风险最小化准则下的最小二乘估计,见公式2.44
对结构风险最小化的目标函数进行求导,得到
由此岭回归的解即为结构风险最小化准则下的最小二乘估计
2-5
在线性回归中,若假设标签,并用最大似然估计来优化参数,验证最优参数为公式2.52的解
写出对数似然函数
将上式对求导,并令其等于0。其中,设对数底数为,得
2-6
假设有个样本服从正态分布,其中未知。
- 使用最大似然估计来求解 最优参数
- 若参数为随机变量,并服从正态分布,使用最大后验估计来求解最优参数
写出对数似然函数:
似然函数对求导,令其等于0,得:
由题有:
通过:
得到最大后验概率估计:
2-7
在习题2-6中,证明当时,最大后验估计趋向于最大似然估计
在
*2.6题(2)中
算了 有点晕,自己说不清楚
网上的解答
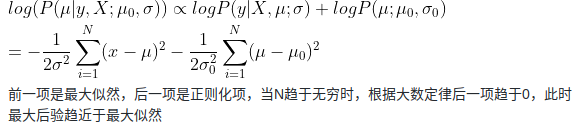
2-8
验证公式2.61
以回归问题为例,假设数据的真实分布为 ,并采用平方损失函数,模型 期望风险为:
这里,我们把期望风险分解一下,加入 ,即数据的真实条件分布,即已知x时y的期望,那么:
这里省略了 ,同时将平方直接拆开了,这个等式里面:
是不变的, 也是不变的,只有 是要学习的模型,是可变的。根据期望风险最小化原则,最小化
即获得最优模型 ,
使上式中第二项第三项为0,即:
即最优模型为:
2-9
试分析什么因素会导致模型出现图2.6所示的高偏差和高方差情况
高偏差原因:
- 数据特征过少;
- 模型复杂度太低;
- 正则化系数λ太大;
高方差原因:
- 数据样例过少;
- 模型复杂度过高;
- 正则化系数λ太小;
- 没有使用交叉验证;
引用自:https://github.com/nndl/solutions/issues/16#issuecomment-691631783
2-10
验证公式2.66

2-11
分别用一元、二元和三元特征的词袋模型表示文本”我打了张三“和”张三打了我“,并分析不同模型的优缺点
一元:
词表: 我 打 了 张 三
x1: [1,1,1,1,1]
x2: [1,1,1,1,1]
二元:
词表: $我 我打 打了 了张 张三 三# $张 三打 了我 我#
x1: [1,1,1,1,1,1,0,0,0,0]
x2: [0,0,1,0,1,0,1,1,1,1]
三元:
词表:$我打 我打了 打了张 了张三 张三# $张三 张三打 三打了 打了我 了我#
x1: [1,1,1,1,1,0,0,0,0,0]
x2: [0,0,0,0,0,1,1,1,1,1]
一元特征的词袋模型词表的特征数量少,同样文本向量的特征数量也少,但是不同顺序的文本容易造成相同的BoW。二元、三元则反之。
2-12
对于一个三分类问题,数据集的真实标签和模型的预测标签如下:
真实标签 1 1 2 2 2 3 3 3 3 预测标签 1 2 2 2 3 3 3 1 2 分别计算模型的精准率、召回率、F1值以及它们的宏平均和微平均
类别1
TP = 1 FN = 1 FP = 1 TN = 3
精准率:p = 1/2
召回率:R= 1/2
F1:1/2
类别2
TP = 2 FN = 1 FP = 2 TN = 5
精准率:1/2
召回率:2/3
F1:4/7
类别3
精准率:2/3
召回率:1/2
F1:4/7
宏平均
P=5/9
R=5/9
F1=5/9
微平均
平均精确率=平均召回率=5/9
F1=5/9